1. 简介
带扩散器叶片的离心式压缩机的横截面视图如图1(a)所示,在距离进气管孔0.5米的测量点上测量的辐射噪音如图1(b)所示。其中,扩散器的数量=12,涡轮叶片的数量=11。该图显示了压缩机涡轮的叶片通过频率(BPF)分量直接影响最大的噪音总量。我们假定BPF分量的增加是由内部共鸣引起的,不过,共鸣的精确机制尚未阐明。
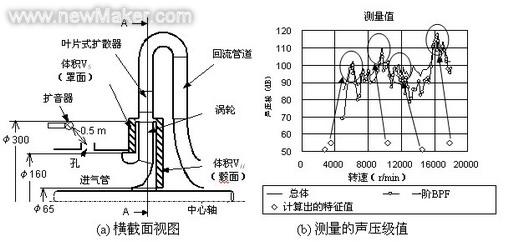
图1 压缩机的横截面视图及其噪音
2. 共鸣机制
BPF噪音是由碰到扩散器叶片的涡轮叶片尾流导致的。这样,扩散器叶片表面上的压力波动就成了BPF噪音源。这些噪音源位于如图2(a)所示的扩散器叶片的逆流边缘。叶片的每个噪音源被假定为点源,这些点源具有相同的源强度以及由涡轮旋转速度引起的不同的相位角。
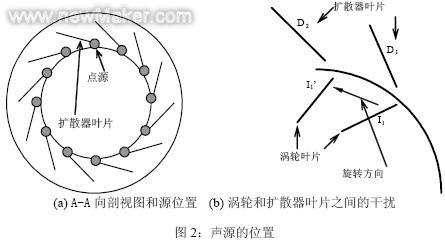
我们根据扩散器叶片D1的点源分别用方程式(1)和方程式(2)计算扩散器叶片D2的点源的时间延迟量T和相位延迟量θ0。
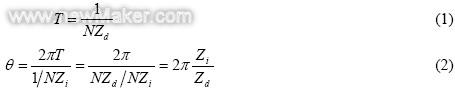
这里,N是以赫兹为单位的涡轮转数,方程式(2)相当于方程式(3)中的θn。相位延迟量θn与方程式(4)中直径节点数mn的激振力相符。
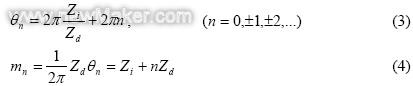
因此,如果与直径节点数mn一致的特征值等于BPF,则可能发生内部共鸣。我们根据以下假设计算节点数mn,即:尾流的行程方向与涡轮的旋转方向相同。我们定义该方向为“前向”,用方程式(5)中的mf替换mn。如果尾流的行程方向为“后向”,相应的直径节点数mB由方程式(6)定义[1]。

通常,内部共鸣发生在封闭的空间内,而不是开放的空间。因此,我们假定离心式压缩机的共鸣发生在涡轮和定子之间的薄薄的圆柱形空间内,这一空间用图1的VS和VH来表示。薄薄的轴向对称空间VS和VH内的声场用方程式(7)表示。将方程式(7)代入到波动方程式(8)中,则得出需要解开的方程式(9)[2]。
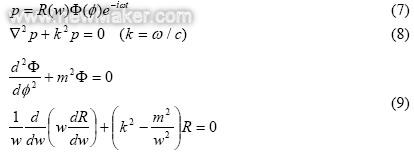
方程式(9)中的Φ通解为cos(mφ)和sin(mφ)(m=0,±1,±2),方程式(9)中R的通解为贝塞尔函数Jm(kw)和诺伊曼函数Nm(kw)。因为假定的共鸣空间有一个半径为w1和w2的圆形刚性边界,所以边界条件的定义如方程式(10)所示。

将方程式(10)中的边界条件代入到方程式(9)中,则得出有数值解的方程式(11)。
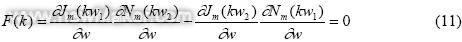
图1(b)中的菱形显示了根据Zi=11、Zd=12时的压缩机方程式(11)计算出的特征值,方程式(5)和方程式(6)中的相应节点数为mF=11、mB=1。在测量范围内计算出的所有特征值与mB=1时的节点相符。计算出的特征值数与试验中的峰值数符合得很好。特征值的差异应归因于边界条件的差异和空间形状。
3. 响应计算
为了验证前面的假定,我们用二维边界元法(BEM)计算了声音响应,计算模型如图3所示。其中,点源位于扩散器叶片的顶部,中心圆是围绕中心轴的边界,所有的边界均假定为刚性。我们计算了在涡轮出口位置Pi(i=1,2,3,4,5)处的声音响应。
在BEM计算中,方程式(12)被用作基本公式。分别用方程式(13)和方程式(14)计算格林函数和来自点源的直接声音分量。
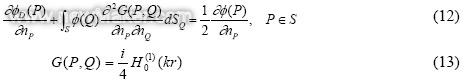
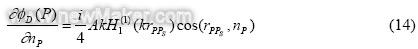
点源的振幅被设为与计算频率的立方成比例,因此可以模拟气动力声源功率增加量的六次方。
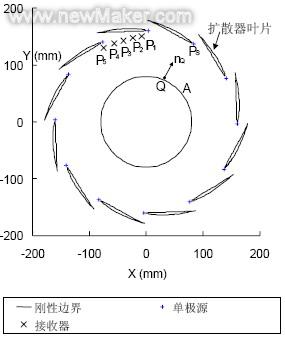
图3:标出源位置和接收器位置(Zd=12)的分析模型
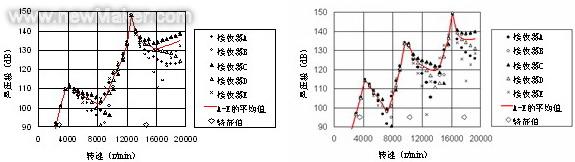
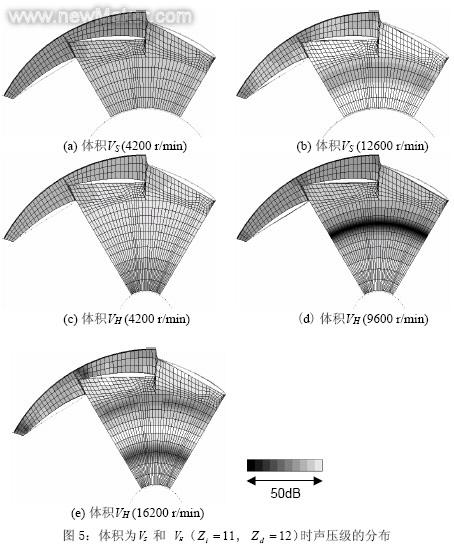
计算出的频率响应如图4所示。结果显示,体积VS和VH的计算结果与图1(b)的试验结果符合得很好。在图4的峰值频率下的声压级分布如图5所示,圆形节点出现在图5(b)、(d)和(e)中。结果显示,这些峰值频率与圆形节点数为0、1、2时的特征模式相符。
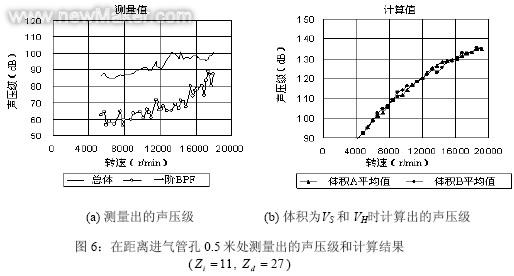
图4的结果与mB=1时的直径节点相符。为了验证这一结果,在不同的扩散器叶片数(Zi=11,Zd=27)下压缩机的计算结果如图6所示。预计的直径节点数为mF=11、mB=16,试验和计算结果均显示没有明显的BPF噪音峰值。
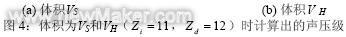
4. 结论
我们开发了如下带扩散器叶片的离心式压缩机内部的声共鸣频率预测方法。
1) 噪音的增加是由在涡轮和定子之间的空间内部的声共鸣引起的。
2) 依据扩散器叶片数和涡轮叶片数,使用贝塞尔函数的方程式可以用于粗略预计共鸣频率。
参考文献
[1]高野靖,小林博美:《离心式压缩机的内部声共鸣》(日文版),日本声音协会,58(4)卷,(2002年)。
[2]P·M·Morse,K·U·Ingard:《理论声学》(Magraw-Hill),356(1968年)。
高野靖
日立有限公司机械工程研究实验室
日本土浦神立路502号,邮编:300-0013
E-mail: y_takano@merl.hitachi.co.jp
小林博美
日立工业有限公司
日本土浦神立路603号,邮编:300-0013
|
